LENS DIFFRACTION & PHOTOGRAPHY
Diffraction is an optical effect which limits the total resolution of your photography — no matter how many megapixels your camera may have. It happens because light begins to disperse or "diffract" when passing through a small opening (such as your camera's aperture). This effect is normally negligible, since smaller apertures often improve sharpness by minimizing lens aberrations. However, for sufficiently small apertures, this strategy becomes counterproductive — at which point your camera is said to have become diffraction limited. Knowing this limit can help maximize detail, and avoid an unnecessarily long exposure or high ISO speed.
BACKGROUND
Light rays passing through a small aperture will begin to diverge and interfere with one another. This becomes more significant as the size of the aperture decreases relative to the wavelength of light passing through, but occurs to some extent for any aperture or concentrated light source.


Since the divergent rays now travel different distances, some move out of phase and begin to interfere with each other — adding in some places and partially or completely canceling out in others. This interference produces a diffraction pattern with peak intensities where the amplitude of the light waves add, and less light where they subtract. If one were to measure the intensity of light reaching each position on a line, the measurements would appear as bands similar to those shown below.

For an ideal circular aperture, the 2-D diffraction pattern is called an "airy disk," after its discoverer George Airy. The width of the airy disk is used to define the theoretical maximum resolution for an optical system (defined as the diameter of the first dark circle).
 Airy Disk
Airy Disk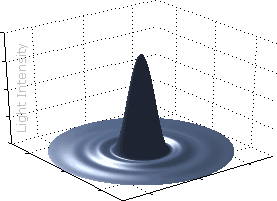 3-D Visualization
3-D VisualizationWhen the diameter of the airy disk's central peak becomes large relative to the pixel size in the camera (or maximum tolerable circle of confusion), it begins to have a visual impact on the image. Once two airy disks become any closer than half their width, they are also no longer resolvable (Rayleigh criterion).
 Barely Resolved
Barely Resolved No Longer Resolved
No Longer ResolvedDiffraction thus sets a fundamental resolution limit that is independent of the number of megapixels, or the size of the film format. It depends only on the f-number of your lens, and on the wavelength of light being imaged. One can think of it as the smallest theoretical "pixel" of detail in photography. Furthermore, the onset of diffraction is gradual; prior to limiting resolution, it can still reduce small-scale contrast by causing airy disks to partially overlap.
VISUAL EXAMPLE: APERTURE VS. PIXEL SIZE
The size of the airy disk is primarily useful in the context of pixel size. The following interactive tool shows a single airy disk compared to pixel size for several camera models:
Note: above airy disk will appear narrower than its specified diameter (since this is defined by where it reaches its first minimum instead of by the visible inner bright region).
As a result of the sensor's anti-aliasing filter (and the Rayleigh criterion above), an airy disk can have a diameter of about 2-3 pixels before diffraction limits resolution (assuming an otherwise perfect lens). However, diffraction will likely have a visual impact prior to reaching this diameter.
As two examples, the Canon EOS 20D begins to show diffraction at around f/11, whereas the Canon PowerShot G6 begins to show its effects at only about f/5.6. On the other hand, the Canon G6 does not require apertures as small as the 20D in order to achieve the same depth of field (due to its much smaller sensor size).
Since the size of the airy disk also depends on the wavelength of light, each of the three primary colors will reach its diffraction limit at a different aperture. The calculation above assumes light in the middle of the visible spectrum (~550 nm). Typical digital SLR cameras can capture light with a wavelength of anywhere from 450 to 680 nm, so at best the airy disk would have a diameter of 80% the size shown above (for pure blue light).
Another complication is that sensors utilizing a Bayer array allocate twice the fraction of pixels to green as red or blue light, and then interpolate these colors to produce the final full color image. This means that as the diffraction limit is approached, the first signs will be a loss of resolution in green and pixel-level luminosity. Blue light requires the smallest apertures (highest f-stop) in order to reduce its resolution due to diffraction.
- The physical pixels do not actually occupy 100% of the sensor area, but instead have gaps in between. This calculation assumes that microlenses make these gaps negligible.
- Some cameras have pixels which are slightly rectangular, in which case diffraction will reduce resolution more in one direction than the other.
- The above chart approximates the aperture as being circular (a common approximation), but in reality these are polygonal with 5-8 sides.
- The calculation for pixel area assumes these extend all the way to the edge of each sensor, and all contribute to the final image. In reality, camera manufacturers leave some pixels unused around the edge of the sensor. Since not all manufacturers specify the number of used vs. unused pixels, only used pixels were considered when calculating the fraction of total sensor area. The pixel sizes above are thus slightly larger than if measured (but by no more than 5%).
WHAT IT LOOKS LIKE
Although the above diagrams help give a feel for the concept of diffraction, only real-world photography can show its visual impact. The following series of images were taken on the Canon EOS 20D, which typically exhibits softening from diffraction beyond about f/11. Move your mouse over each f-number to see how these impact fine detail:

| Select Aperture: | f/8.0 | f/11 | f/16 | f/22 |
 No Overlap of Airy Disks
No Overlap of Airy Disks
 Partial Overlap of Airy Disks
Partial Overlap of Airy Disks
Note how most of the lines in the fabric are still resolved at f/11, but have slightly lower small-scale contrast or acutance (particularly where the fabric lines are very close). This is because the airy disks are only partially overlapping, similar to the effect on adjacent rows of alternating black and white airy disks (as shown on the right). By f/22, almost all fine lines have been smoothed out because the airy disks are larger than this detail.
CALCULATING THE DIFFRACTION LIMIT
The form below calculates the size of the airy disk and assesses whether the camera has become diffraction limited. Click on "show advanced" to define a custom circle of confusion (CoC), or to see the influence of pixel size.
Note: CF = "crop factor" (commonly referred to as the focal length multiplier); assumes square pixels, 4:3 aspect ratio for compact digital and 3:2 for SLR. *Calculator assumes that your camera sensor uses the typical bayer array.
This calculator shows a camera as being diffraction limited when the diameter of the airy disk exceeds what is typically resolvable in an 8x10 inch print viewed from one foot. Click "show advanced" to change the criteria for reaching this limit. The "set circle of confusion based on pixels" checkbox indicates when diffraction is likely to become visible on a computer at 100% scale. For a further explanation of each input setting, also see the depth of field calculator.
In practice, the diffraction limit doesn't necessarily bring about an abrupt change; there is actually a gradual transition between when diffraction is and is not visible. Furthermore, this limit is only a best-case scenario when using an otherwise perfect lens; real-world results may vary.
NOTES ON REAL-WORLD USE IN PHOTOGRAPHY
Even when a camera system is near or just past its diffraction limit, other factors such as focus accuracy, motion blur and imperfect lenses are likely to be more significant. Diffraction therefore limits total sharpness only when using a sturdy tripod, mirror lock-up and a very high quality lens.
Some diffraction is often ok if you are willing to sacrifice sharpness at the focal plane in exchange for sharpness outside the depth of field. Alternatively, very small apertures may be required to achieve sufficiently long exposures, such as to induce motion blur with flowing water. In other words, diffraction is just something to be aware of when choosing your exposure settings, similar to how one would balance other trade-offs such as noise (ISO) vs shutter speed.
This should not lead you to think that "larger apertures are better," even though very small apertures create a soft image; most lenses are also quite soft when used wide open (at the largest aperture available). Camera systems typically have an optimal aperture in between the largest and smallest settings; with most lenses, optimal sharpness is often close to the diffraction limit, but with some lenses this may even occur prior to the diffraction limit. These calculations only show when diffraction becomes significant, not necessarily the location of optimum sharpness (see camera lens quality: MTF, resolution & contrast for more on this).
Are smaller pixels somehow worse? Not necessarily. Just because the diffraction limit has been reached (with large pixels) does not necessarily mean an image is any worse than if smaller pixels had been used (and the limit was surpassed); both scenarios still have the same total resolution (even though the smaller pixels produce a larger file). However, the camera with the smaller pixels will render the photo with fewer artifacts (such as color moiré and aliasing). Smaller pixels also give more creative flexibility, since these can yield a higher resolution if using a larger aperture is possible (such as when the depth of field can be shallow). On the other hand, when other factors such as noise and dynamic range are considered, the "small vs. large" pixels debate becomes more complicated...
Technical Note: Independence of Focal Length Since the physical size of an aperture is larger for telephoto lenses (f/4 has a 50 mm diameter at 200 mm, but only a 25 mm diameter at 100 mm), why doesn't the airy disk become smaller? This is because longer focal lengths also cause light to travel farther before hitting the camera sensor -- thus increasing the distance over which the airy disk can continue to diverge. The competing effects of larger aperture and longer focal length therefore cancel, leaving only the f-number as being important (which describes focal length relative to aperture size).
For additional reading on this topic, also see the addendum: Digital Camera Diffraction, Part 2: Resolution, Color & Micro-Contrast



