PANORAMIC IMAGE PROJECTIONS
An image projection occurs whenever a flat image is mapped onto a curved surface, or vice versa, and is particularly common in panoramic photography. A projection is performed when a cartographer maps a spherical globe of the earth onto a flat piece of paper, for example. Since the entire field of view around us can be thought of as the surface of a sphere (for all viewing angles), a similar spherical to 2-D projection is required for photographs which are to be printed.
 Narrow Angle of View
Narrow Angle of View(grid remains nearly square)
 Wider Angle of View
Wider Angle of View(grid is highly distorted)
For small viewing angles, it is relatively easy to distort this into an image on a flat piece of paper since this viewing arc is relatively flat. Some distortion is inevitable when trying to map a spherical image onto a flat surface, therefore each projection type only tries to minimize one type of distortion at the expense of others. As the viewing angle increases, the viewing arc becomes more curved, and thus the difference between panorama projection types becomes more pronounced. When to use each projection depends largely on the subject matter and application; here we focus on a few which are most commonly encountered in digital photography. Many of the projection types discussed in this tutorial are selectable as an output format for several panoramic software packages; PTAssembler allows selection of all those which are listed.
IMAGE PROJECTION TYPES IN PHOTOGRAPHY
 Grid Representing Sphere of Vision
Grid Representing Sphere of Vision(if standing at center)
 Projection Type for Flattened Sphere:
Projection Type for Flattened Sphere:
| Equirectangular (100% Coverage) | |
| Rectilinear | Cylindrical |
| Mercator | Fisheye |
| Sinusoidal | Stereographic |
If all the above image projection types seem a bit daunting, try to first just read and understand the distinction between rectilinear and cylindrical (shown in bold), as these are the ones which are most widely used when photo stitching digital panoramas.
Equirectangular image projections map the latitude and longitude coordinates of a spherical globe directly onto horizontal and vertical coordinates of a grid, where this grid is roughly twice as wide as it is tall. Horizontal stretching therefore increases farther from the poles, with the north and south poles being stretched across the entire upper and lower edges of the flattened grid. Equirectangular projections can show the entire vertical and horizontal angle of view up to 360 degrees.
Cylindrical image projections are similar to equirectangular, except it also vertically stretches objects as they get closer to the north and south poles, with infinite vertical stretching occurring at the poles (therefore no horizontal line is shown at the top and bottom of this flattened grid). It is for this reason that cylindrical projections are also not suitable for images with a very large vertical angle of view. Cylindrical projections are also the standard type rendered by traditional panoramic film cameras with a swing lens. Cylindrical projections maintain more accurate relative sizes of objects than rectilinear projections, however this is done at the expense of rendering lines parallel to the viewer's line of sight as being curved (even though these would otherwise appear straight).
Rectilinear image projections have the primary advantage that they map all straight lines in three-dimensional space to straight lines on the flattened two-dimensional grid. This projection type is what most ordinary wide angle lenses aim to produce, so this is perhaps the projection with which we are most familiar. Its primary disadvantage is that it can greatly exaggerate perspective as the angle of view increases, leading to objects appearing skewed at the edges of the frame. It is for this reason that rectilinear projections are generally not recommended for angles of view much greater than 120 degrees.
Fisheye image projections aim to create a flattened grid where the distance from the center of this grid is roughly proportional to actual viewing angle, yielding an image which would look similar to the reflection off of a metallic sphere. These are generally not used as an output format for panoramic photography, but may instead represent the input images when the camera lens type being used for photo stitching is a fisheye lens. Fisheye projections are also limited to vertical and horizontal angles of view of 180 degrees or less, yielding an image which fits within a circle. This would be characterized by (otherwise straight) lines becoming progressively more curved the farther they get from the center of the image grid. A camera with a fisheye lens is extremely useful when creating panoramas that encompass the entire sphere of vision, since these often require stitching just a few input photographs.
Mercator image projections are most closely related to the cylindrical and equirectangular projection types; mercator represents a compromise between these two types, providing for less vertical stretching and a greater usable vertical angle of view than cylindrical, but with more line curvature. This projection is perhaps the most recognizable from its use in flat maps of the earth. Here we also note that an alternative form of this projection (the transverse mercator) may be used for very tall vertical panoramas.
Sinusoidal image projections aim to maintain equal areas throughout all grid sections. If flattening the globe of an earth, one can imagine that this projection could be rolled back up again to form a sphere with the same area and shape as the original. The equal area characteristic is useful because if recording a spherical image in 2-D, it maintains the same horizontal and vertical resolution throughout the image. This projection is similar to the fisheye and stereographic types, except that it maintains perfectly horizontal latitude lines from the original sphere.
Stereographic image projections are very similar to fisheye projections, except that it maintains a better sense of perspective by progressively stretching objects away from the point of perspective. This perspective-exaggerating characteristic is somewhat similar to that yielded by the rectilinear projection, though certainly less pronounced.
EXAMPLES: WIDE HORIZONTAL FIELD OF VIEW
How do the above image projections actually influence a panoramic photograph? The following series of photographs are used to visualize the difference between two projection types most often encountered in photo stitching software: rectilinear and cylindrical projections. These are designed to show only distortion differences for a wide horizontal angle of view; vertical panoramas are used later on to illustrate differences in vertical distortion between other projection types.

The first example demonstrates how a rectilinear image projection would be rendered in a photo stitch of the above three photographs.
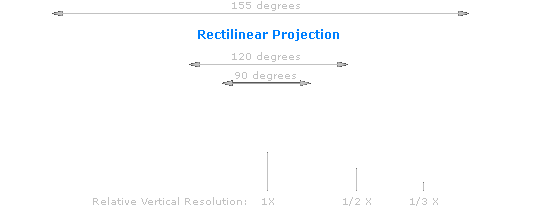
Note the extreme distortion near the edges of the angle of view, in addition to the dramatic loss in resolution due to image stretching. The next image demonstrates how the highly distorted image above would appear if it were cropped to contain just a 120 degree horizontal angle of view.

Here we see that this cropped rectilinear projection yields a very suitable look, since all straight architectural lines are rendered straight in the stitched photograph. On the other hand, this is done at the expense of maintaining the relative size of objects throughout the angle of view; objects toward the edge of the angle of view (far left and right) are significantly enlarged compared to those at the center (tower with doorway at base).
The next example demonstrates how the stitched photographs would appear using a cylindrical projection. Cylindrical projections also have the advantage of producing stitched photographs with relatively even resolution throughout, and also require minimal cropping of empty space. Additionally, the difference between cylindrical and equirectangular is negligible for photographs which do not have extreme vertical angles of view (such as the example below).


EXAMPLES: TALL VERTICAL FIELD OF VIEW
The following examples illustrate the difference between projection types for a vertical panorama (with a very large vertical field of view). This gives a chance to visualize the difference between the equirectangular, cylindrical and mercator projections, even though these would have appeared the same in the previous example (with a wide horizontal angle of view).
 Cylindrical
Cylindrical
 Mercator
Mercator
 Equirectangular
Equirectangular
Note: Vertical compression increases from left to right. The point of perspective was set as the base of the tower, therefore the effective vertical angle of view looks as if there were a 140 degrees field of view in total (if the perspective point were at the halfway height).


This large vertical angle of view allows us to clearly see how each of these image projections differ in their degree of vertical stretching/compression. The equirectangular projection compresses vertical perspective so greatly that one arguably loses the sense of extreme height that this tower gives in person. For this reason, equirectangular is only recommended when absolutely necessary (such as in stitched photographs with both an extreme vertical and horizontal field of view).
The three projections above aim to maintain nearly straight vertical lines; the transverse mercator projection to the right sacrifices some curvature for a (subjectively) more realistic perspective. This projection type is often used for panoramas with extreme vertical angles of view. Also note how this projection closely mimics the look of each of the individual source photographs.
The difference between rectilinear and cylindrical is barely noticeable for this narrow horizontal angle of view, so the rectilinear projection was not included.
PANORAMIC FIELD OF VIEW CALCULATORS
The following calculator can be used to estimate your camera's vertical and horizontal angles of view for different lens focal lengths, which can help in assessing which projection type would be most suitable.
Note: Calculators not intended for use in extreme macro photography. The above results are only approximate, since the angle of view is actually also influenced (to a lesser degree) by the focusing distance. Additionally, field of view estimate assumes that the lens performs a perfect rectilinear image projection; lenses with large barrel or pincushion distortion may yield slightly different results.
The next calculator estimates how many photos are required to encompass a 360 degree horizontal field of view, given the input settings of: focal length, camera orientation, photo overlap and digital camera sensor size.
Note: CF = crop factor, which describes the relative width of the camera sensor compared to a 35 mm camera. For a background reading, please visit the tutorial on digital camera sensor sizes.
For a summary of when to consider each projection type, please refer to the table below:
| Projection Type | Field of View Recommendations | Straight Lines? | ||
|---|---|---|---|---|
| Horizontal | Vertical | Horizontal | Vertical | |
| Rectilinear | <120° | <120° | YES | YES |
| Cylindrical | ~120-360° | <120° | NO | YES |
| Mercator | ~120-360° | <150° | NO | YES |
| Equirectangular | ~120-360° | 120-180° | NO | YES |
| Fisheye | <180° | <180° | NO | NO |
Note: All straight line considerations exclude the centermost horizontal and vertical lines, and fields of view assume that the point of perspective is located at the center of this angle.
For background reading on creating digital panoramas, please also refer to:
Part 1: Photo Stitching Digital Panoramas
Part 2: Using Photo Stitching Software






